很多同学在调试小车的时候会遇到这样一个问题:为什么我的小车总是走歪,走不了直线呢?由于电机和车轮还有摩擦阻力等问题,两个车轮的转速不可能总是相等,于是便出现小车走着走着,便歪了的情况。这就要靠我们的程序来调整了。


试想这样一种情况,地面上有一条笔直的黑色电工胶带,有一辆在车的正前方安装了一个红外对管的小车。现在我希望小车沿着这条胶带与白色区域的交界走(为什么不是胶带的中央呢?因为如果小车走偏,红外对管虽然检测到白色区域,却不知道是左偏还是右偏)。红外对管的左侧是白色,右边是黑色,左边的电机称为A,右边的为C。如图所示。
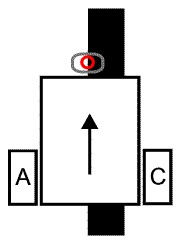
假设红外对管可以给所连接的单片机返回一个40到50的数。45表示黑白交界处,小于45表示白色,大于45表示黑色,且数值与45差的绝对值越大表示越远离交界处(实际情况可能有所不同)。很显然,我们总是希望它返回45,而返回40到44时,小车应该右转,返回46到50时,小车应该左转。具体到电机就是返回40到44时,A加速,C减速,返回46到50同理。
具体加(减)速多少呢?我们将45设置为标准,设红外对管返回值为a,令e=45-a,规定e是误差值,显然e为正就应该右转,为负左转。假设实验中A,C初始速度均为50。将e乘以一个比例系数Kp,换算成要调整的电机速度。那么A的速度就是50+Kp*e,C的速度为50-Kp*e。
这便是PID中的P,即比例控制,Kp称为比例增益,其值的确定需要在实验中不断调整。
假设我在一次实验中得到的一组连续的误差是2,3,2,2,3,很显然小车一直偏向左,而P控制却没有及时纠正。如果将这组数据求和,再乘以一个另一个比例系数Ki,加到刚才的式子中,让电机调整,会出现什么情况呢?电机知道自己过去走得太偏了,于是加大调整速度,终于重回正轨!
上述便是PID中的I,即积分控制,Ki称为积分增益,其值的确定同样需要在实验中不断调整。举的例子只是误差简单的求和,实际上积分控制中还需要用误差乘以dt再求和。积分下限是0,即开始,上限是现在的时间,被积函数是e(t),也就是误差随时间变化的函数,对时间积分,统计从开始一直到现在的误差。
总结一下,P代表现在,I代表过去。可以想到,D代表将来。
假设我在一次实验中得到的一组连续的误差是5,3,1,你猜下一个是多少?没错是-1,通过等差数列的知识可以轻松预测。同样的道理,如果小车预测到它下一步会发生什么,就能更好地做出调整了。在刚才的例子中,小车一直偏左,但是越来越靠近中间了,如果不加以控制可能又会偏右。而如果小车预测到了这个情况,及时将A减速,并将C加速,就不会偏太多了。
简单来说,将这次的误差减去上次的误差,再乘以一个比例系数Kd就是D,即微分控制。 也可以简单理解为导数,那一点的切线斜率表示变化趋势。
综上,我们终于得到了PID的表达式:
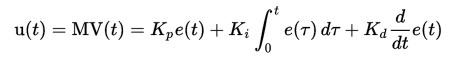
在这次比赛中,不一定要用PID三项控制,因为这样需要调整三个系数,非常麻烦。可能PI就够了,也可能是PD,甚至P就够了。总之,适合自己小车的算法才是最好的!


